Network Science - UDD

Network Projections

Cristian Candia-Castro Vallejos, Ph.D. $^{1, 2}$

Yessica Herrera-Guzmán, Ph.D. $^{2, 3}$

[1] Data Science Institute (IDS), Universidad del Desarrollo,Chile
[2] Northwestern Institute on Complex Systems, Kellogg School of Management, Northwestern Unviersity, USA
[3] Center for Complex Network Research (CCNR), Northwestern Unviersity, USA

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
%matplotlib inline

import networkx as nx

Número de personas que contrajeron COVID

Este es un conjunto de datos generado aleatoriamente para ilustrar la construcción de redes bipartitas a partir de conjuntos de datos tabulares empíricos.

En este conjunto de datos, hay variantes de COVID y los nombres enumerados para cada variante son aquellos que fueron infectados con esa variante.

El objetivo de esta práctica es que te familiarices con este tipo de datos estructurados que no están en forma de lista de aristas, sino que se asemejan a fuentes de datos de investigaciones empíricas. A partir de estos datos, deberías ser capaz de crear una red bipartita, así como la lista de nodos y la lista de aristas para cada una de las proyecciones de la red.

data = pd.read_csv('./Data/COVIDvariants.csv')

data.head()

	Variant1	Variant2	Variant3	Variant4	Variant5	Variant6	Variant7	Variant8	Variant9	Variant10
0	Charlie	Frank	Quinn	Oliver	Charlie	Helen	Grace	Rachel	Michael	Grace
1	Sam	David	David	Nina	Nadia	Bob	Ivy	Laura	Tina	Ronald
2	Nina	Oliver	Charlie	Helen	Paul	Eva	Quinn	Sam	Ivy	Bob
3	Alice	Quinn	Bob	Quinn	Sam	Jack	Kevin	Michael	Frank	Nina
4	Kevin	Sam	Rachel	Jack	Kevin	Frank	Eva	Alice	Quinn	Laura

Convert the dataset to the edgelist of a bipartite network, where one level (col1 = ‘variant’) are the variants and another level (col2 = ‘name’) are the infected individuals.

df = data.melt(var_name='variant', value_name='name').dropna()

df

	variant	name
0	Variant1	Charlie
1	Variant1	Sam
2	Variant1	Nina
3	Variant1	Alice
4	Variant1	Kevin
...	...	...
395	Variant10	Sarah
396	Variant10	Paula
397	Variant10	Ted
398	Variant10	Arthur
399	Variant10	Robert

221 rows × 2 columns

g = nx.Graph()

g = nx.from_pandas_edgelist(df, source='variant', target='name')

# print(nx.info(g))
print(g)

Graph with 69 nodes and 221 edges

g.degree('Ivy')

g.degree('Variant1')

variants = list(df.variant.unique())

people = list(df.name.unique())

layout = nx.spring_layout(g, k=0.05, iterations=50)

plt.figure(figsize=(12, 12))

# Draw VARIANTS
nx.draw_networkx_nodes(g, 
                       layout, 
                       nodelist=variants, 
                       node_size=80, # a LIST of sizes, based on g.degree
                       node_color='green',
                       edgecolors='green', 
                       linewidths=1.5)


# Draw EVERYONE
nx.draw_networkx_nodes(g, layout, nodelist=people, 
                       node_color='navy', 
                       edgecolors='navy',
                       alpha=0.9,
                       linewidths=0.7, 
                       node_size=20)


# Draw REINFECTED PEOPLE
reinfected_people = [person for person in people if g.degree(person) > 1]
nx.draw_networkx_nodes(g, layout, nodelist=reinfected_people, 
                       node_color='red', 
                       edgecolors='navy',
                       linewidths=0.7,
                       node_size=40)

nx.draw_networkx_edges(g, layout, width=0.7, alpha=0.9,
                       edge_color="limegreen")

# # label people
# node_labels = dict(zip(people, people))
# nx.draw_networkx_labels(g, layout, labels=node_labels,
#                        font_size=8, font_weight='400')


# # label variants
# node_variants = dict(zip(variants, variants))
# nx.draw_networkx_labels(g, layout, labels=node_variants,
#                        font_size=12, font_weight='400')



# Turn off the axis because I know you don't want it
plt.axis('off')

plt.title("Network of COVID variants")
# plt.savefig('network_name.pdf', bbox_inches='tight', pad_inches=0)
# Tell matplotlib to show it
plt.show()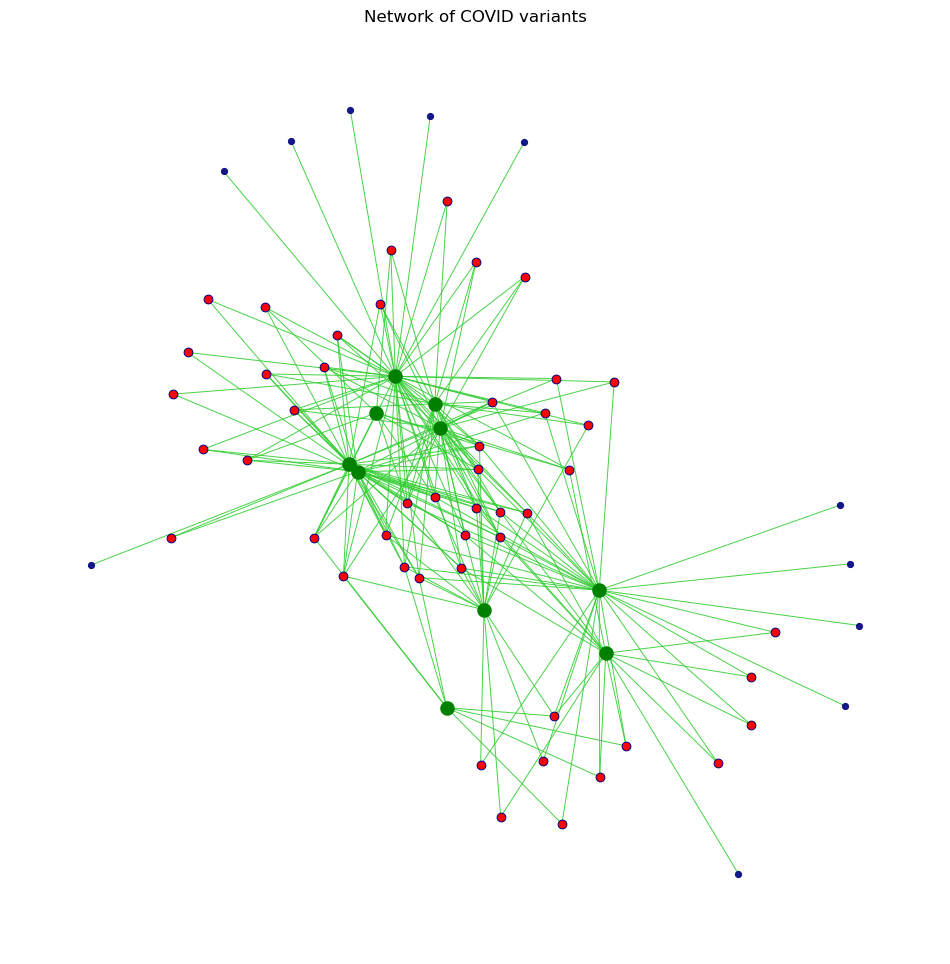

Tarea

Pregunta 1: ¿Cuál es la naturaleza de la relación entre los dos conjuntos de nodos en la red bipartita?

Pregunta 2: ¿Existen medidas específicas para la centralidad e influencia de nodos en redes bipartitas?

Pregunta 3: ¿Cuáles son las redes proyectadas de cada conjunto de nodos? (es decir, redes separadas para cada conjunto)

Ejercicio: Construye la matriz de adyacencia de sus dos proyecciones, en los nodos morados y en los nodos verdes, respectivamente. Vea el ejemplo a continuación. Luego, explique la relevancia de cada proyección.

Project to unipartite: Infected people

wide_df = df.pivot_table(index='variant', columns=df.groupby('variant').cumcount(), values='name', aggfunc='first')

wide_df.columns = [f'Name{i+1}' for i in range(wide_df.shape[1])]

# Initialize empty lists to store source and target names
source = []
target = []

# Iterate through DataFrame rows
for index, row in wide_df.iterrows():
    # Iterate through column names in the current row
    for i, name1 in enumerate(row):
        for j, name2 in enumerate(row[i+1:]):
            # Append source and target names to the lists
            source.append(name1)
            target.append(name2)

# Create a new DataFrame from the source and target lists
people_df = pd.DataFrame({'Source': source, 'Target': target})

people_df = people_df.dropna()

new_df = people_df.drop_duplicates()

new_df = new_df[new_df['Source'] != new_df['Target']]

h = nx.from_pandas_edgelist(new_df, source='Source', target='Target')

print(nx.info(h))

Graph with 59 nodes and 1265 edges

layout_h = nx.spring_layout(h, k=0.1, iterations=50)

labels = {node: h.nodes[node].get('label', f'Node {node}') for node in h.nodes}

plt.figure(figsize=(12, 12))

nx.draw_networkx_nodes(h, 
                       layout_h, 
                       node_size=[(h.degree(v)) ** 2 for v in h.nodes()], # sizes based on h.degree
                       node_color='lavender',
                       edgecolors='rebeccapurple',
                       linewidths=1)


nx.draw_networkx_edges(h, layout_h, width=0.4, alpha=0.7, edge_color="gray")


node_labels = dict(zip(labels, labels))
nx.draw_networkx_labels(h, layout_h, labels=node_labels,
                       font_size=8)


plt.axis('off')
plt.title("Network of Infected People")
# plt.savefig('network_projection_name.pdf', bbox_inches='tight', pad_inches=0)
plt.show()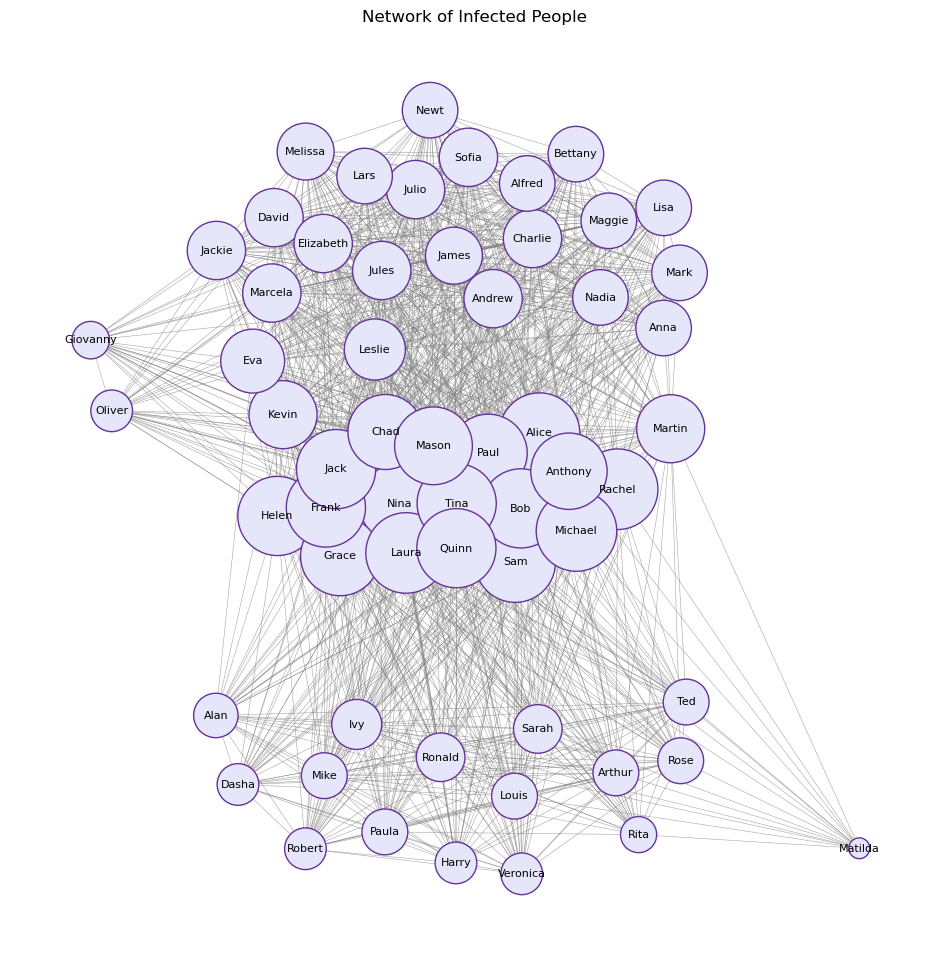

Tarea

Pregunta 1: ¿Cuáles son las redes proyectadas de cada conjunto de nodos? (es decir, redes separadas para cada conjunto)

Pregunta 2: ¿Qué información puedes obtener de cada proyección?

Pregunta 3: Explica la utilidad de las proyecciones de redes con respecto a la visualización y análisis de la red bipartita.

Ejercicio 1: Calcula el grado promedio de cada proyección de la red, luego calcula el grado promedio de los nodos morados y los nodos verdes en la red bipartita. ¿Cuáles son las diferencias en la distribución? Por favor, explica por qué.

Ejercicio 2: Computa las propiedades de estas redes proyectadas (por ejemplo, tamaño, densidad, diámetro, distribución de grados).

Ejercicio 3: Explora visualmente subgrupos o comunidades densamente conectados dentro de las proyecciones. ¿Cómo se relacionan los subgrupos densamente conectados en cada proyección con la red bipartita original?

Network Projections

Cristian Candia-Castro Vallejos, Ph.D.1,2

Yessica Herrera-Guzmán, Ph.D.2,3

Número de personas que contrajeron COVID

Tarea

Tarea

Cristian Candia-Castro Vallejos, Ph.D. $^{1, 2}$

Yessica Herrera-Guzmán, Ph.D. $^{2, 3}$