Network Science - UDD

Básicos en redes

Cristian Candia-Castro Vallejos, Ph.D.

Universidad del Desarrollo (UDD), Chile

• Director at the Computational Research in Social Sciences Laboratory (CRiSS-Lab)

• Faculty, Data Science Institute, School of Engineering

• Faculty, Center for Social Complexity, School of Government

Northwestern University, United States

• External Faculty, Northwestern Institute on Complex Systems (NICO) Kellogg School of Management.

Importando Modulos Requeridos

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl

import networkx as nx

# !pip install networkx

# default settings para plotear Redes
mpl.rc('xtick', labelsize=14, color="#222222") 
mpl.rc('ytick', labelsize=14, color="#222222") 
mpl.rc('font', **{'family':'sans-serif','sans-serif':['Arial']})
mpl.rc('font', size=16)
mpl.rc('xtick.major', size=6, width=1)
mpl.rc('xtick.minor', size=3, width=1)
mpl.rc('ytick.major', size=6, width=1)
mpl.rc('ytick.minor', size=3, width=1)
mpl.rc('axes', linewidth=1, edgecolor="#222222", labelcolor="#222222")
mpl.rc('text', usetex=False, color="#222222")

Tipos básicos de data en NetworkX

NetworkX proporciona las siguientes clases que representan datos relacionados con la red, así como algoritmos de análisis de red que operan en estos objetos:

Graph - Grafos no dirigidos con auto-loops

DiGraph - Grafos dirigidos con auto-loops

MultiGraph - Grafo no-dirigidos con auto-loops y enlaces múltiples

MultiDiGraph - Grafos dirigidos con auto-loops y enlaces múltiples

Comencemos

Crea una red vacía y no-dirigida

G = nx.Graph()

G

<networkx.classes.graph.Graph at 0x1199a2470>

G.nodes()

NodeView(())

Nodos

Los nodos pueden ser casi cualquier cosa, incluyendo nombres, strings, coordenadas GPS, tú los nombras!

Es posible agregar nodos uno a la vez:

G.add_node(0)

G.add_node("Juan")

# objeto tupla representando, por ejemplo, longitud y latitud
G.add_node((1.2, 3.4))

G.nodes()

NodeView((0, 'Juan', (1.2, 3.4)))

… o muchos a la vez desde un contenedor de python

# [1,2,3] es una lista que contiene 1, 2 y 3
G.add_nodes_from([1, 2, 3,"Carlos"])

G.nodes()

NodeView((0, 'Juan', (1.2, 3.4), 1, 2, 3, 'Carlos'))

Atributos de los Nodos

Los nodos pueden tener atributos arbitrarios asociados a ellos, contenidos en un diccionario string-index

Agragar atributos en el momento en que creamos un nodo usando argumentos:

G.add_node("Jorge", color_ojos='verdes', estatura=175)

G.nodes(data=True)

NodeDataView({0: {}, 'Juan': {}, (1.2, 3.4): {}, 1: {}, 2: {}, 3: {}, 'Carlos': {}, 'Jorge': {'color_ojos': 'verdes', 'estatura': 175}})

Tambien puedes agregar atributos a un nodo existente:

G.add_node("Camila")
G.nodes['Camila']

{}

G.nodes["Camila"]["color_ojos"] = "rojo"
G.nodes["Camila"]["edad"] = "23"

G.nodes["Camila"]

{'color_ojos': 'rojo', 'edad': '23'}

G.nodes(data=True)

NodeDataView({0: {'color_ojos': 'rojo'}, 'Juan': {}, (1.2, 3.4): {}, 1: {}, 2: {}, 3: {}, 'Carlos': {}, 'Jorge': {'color_ojos': 'verdes', 'estatura': 175}, 'Camila': {'color_ojos': 'rojo', 'edad': '23'}})

G.add_node("Camila")#, color_ojos='verdes', estatura=175)

G.nodes(data=True)

NodeDataView({0: {'color_ojos': 'rojo'}, 'Juan': {}, (1.2, 3.4): {}, 1: {}, 2: {}, 3: {}, 'Carlos': {}, 'Jorge': {'color_ojos': 'verdes', 'estatura': 175}, 'Camila': {'color_ojos': 'rojo', 'edad': '23'}})

G.node[n] da un diccionario que contiene todos los atributos: pares de valores asociados con el nodo n

print("Los ojos de Jorge son ", G.nodes["Jorge"]["color_ojos"], "y el mide ", G.nodes['Jorge']['estatura'], " centímetros.")
print("Camila tiene los ojos de color", G.nodes["Camila"]["color_ojos"], ".")

Los ojos de Jorge son  verdes y el mide  175  centímetros.
Camila tiene los ojos de color rojo .

Enlaces

Un enlace entre el nodo 1 y el nodo 2 es representado por una tupla (nodo 1, nodo 2).

Ellos pueden ser agregados uno a la vez:

# agrega un enlace entre el nodo 0 y el nodo 1
G.add_edge(0, 1)
G.add_edge('Camila', 100)

G.nodes(data=True)

NodeDataView({0: {'color_ojos': 'rojo'}, 'Juan': {}, (1.2, 3.4): {}, 1: {}, 2: {}, 3: {}, 'Carlos': {}, 'Jorge': {'color_ojos': 'verdes', 'estatura': 175}, 'Camila': {'color_ojos': 'rojo', 'edad': '23'}, 100: {}})

G.edges()

EdgeView([(0, 1), ('Camila', 100)])

O mucho a la vez desde un contenedor:

edge_list = [ (2, 1), ("Jorge", "Camila"), (3, 4), ("A","B") ]

G.add_edges_from(edge_list)

print(G.edges())
# print(G.nodes())

[(0, 1), (1, 2), (3, 4), ('Jorge', 'Camila'), ('Camila', 100), ('A', 'B')]

Nota: Los nodos será creados automáticamente si ellos no existen aún.

Atributos de los Enlaces

Como para los nodos, los enlaces pueden tener atributos arbitrarios. Un atributo importante y especial (para muchos algoritmos) es el “peso”

La sintaxis para agregar/accesar a los atributos de los enlaces es similar a la de los nodos:

G.add_edge("Jorge", "Claudia", weight=10) # weight en general es un string reservado para algunos algortimos de cerntralidad y comunidades en red.
G.add_edge("Jorge", "Claudia", distancia=20)

G.add_edge("Concepcion", "Santiago")

G.add_edge("Concepcion","Santiago", distancia=510)

print(G.edges(data=True))
print('----')
print(G.edges["Concepcion","Santiago"])

[(0, 1, {}), (1, 2, {}), (3, 4, {}), ('Jorge', 'Camila', {}), ('Jorge', 'Claudia', {'weight': 10, 'distancia': 20}), ('Camila', 100, {}), ('A', 'B', {}), ('Concepcion', 'Santiago', {'distancia': 510})]
----
{'distancia': 510}

G.edges['node1','node2'] es un diccionario que contiene todos los atributos: pares de valores asociados con el enlace del nodo 1 al nodo 2.

Operaciones Básicas

Tamaño de la red

# Número de nodos
print(G.number_of_nodes())

# alternativa
print(len(G))

####################

# Número de enlaces
print(G.number_of_edges())

# alternativa
print(G.size())

########################
# cómo hacer formateo de strings
print("El grafo G tiene {0} nodos y {1} enlaces.".format(len(G), G.size()))

16
16
8
8
El grafo G tiene 16 nodos y 8 enlaces.

Testeando si nodos y enlaces existen

G.has_node("Jorge")

True

Alternativa pythonica

"Claudia" in G

True

Para los enlaces, tu debes usar has_edges (no hay una sintaxisis como para nos lodos edge in G) =(

print(G.has_edge(3, 4))
print(G.has_edge("Jorge", 0))

True
False

Encontrando los vecinos de un nodo

print(list(G.neighbors("Camila")))
print(list(G.neighbors(1)))

[100, 'Jorge']
[0, 2]

• En un objeto DiGraph, G.neighbors(node) entrega el nodo sucesor de node, como lo hace G.successors(node) (enlace out)
• Predecesores de node pueden ser obtenidos con G.predecessors(node)

Iterando sobre los nodos y enlaces

Nodos y enlaces pueden ser iterados con G.nodes() y G.edges() respectivamente.

list(G.nodes(data=True))

[(0, {'color_ojos': 'rojo'}),
 ('Juan', {}),
 ((1.2, 3.4), {}),
 (1, {}),
 (2, {}),
 (3, {}),
 ('Carlos', {}),
 ('Jorge', {'color_ojos': 'verdes', 'estatura': 175}),
 ('Camila', {'color_ojos': 'rojo', 'edad': '23'}),
 (100, {}),
 (4, {}),
 ('A', {}),
 ('B', {}),
 ('Claudia', {}),
 ('Concepcion', {}),
 ('Santiago', {})]

for nodo, atributos in list(G.nodes(data=True)): # data=True incluye atributos de nodo como diccionarios
    print("Nodo {0}\t\t\t: {1}".format(nodo, atributos))

Nodo 0          : {'color_ojos': 'rojo'}
Nodo Juan           : {}
Nodo (1.2, 3.4)         : {}
Nodo 1          : {}
Nodo 2          : {}
Nodo 3          : {}
Nodo Carlos         : {}
Nodo Jorge          : {'color_ojos': 'verdes', 'estatura': 175}
Nodo Camila         : {'color_ojos': 'rojo', 'edad': '23'}
Nodo 100            : {}
Nodo 4          : {}
Nodo A          : {}
Nodo B          : {}
Nodo Claudia            : {}
Nodo Concepcion         : {}
Nodo Santiago           : {}

list(G.edges(data=True))

[(0, 1, {}),
 (1, 2, {}),
 (3, 4, {}),
 ('Jorge', 'Camila', {}),
 ('Jorge', 'Claudia', {'weight': 10, 'distancia': 20}),
 ('Camila', 100, {}),
 ('A', 'B', {}),
 ('Concepcion', 'Santiago', {'distancia': 510})]

for n1, n2, atributo in list(G.edges(data=True)):
    print("El primer nodo {0} <----> con el nodo {1}: el atributo es {2}".format(n1, n2, atributo))

El primer nodo 0 <----> con el nodo 1: el atributo es {}
El primer nodo 1 <----> con el nodo 2: el atributo es {}
El primer nodo 3 <----> con el nodo 4: el atributo es {}
El primer nodo Jorge <----> con el nodo Camila: el atributo es {}
El primer nodo Jorge <----> con el nodo Claudia: el atributo es {'weight': 10, 'distancia': 20}
El primer nodo Camila <----> con el nodo 100: el atributo es {}
El primer nodo A <----> con el nodo B: el atributo es {}
El primer nodo Concepcion <----> con el nodo Santiago: el atributo es {'distancia': 510}

Calculando grados

# one node
print(G.degree("Jorge")) # retorna un entero

# todos los nodos (retorna un diccionario con pares nodo : grado para todos los nodos)
print(G.degree())

# solo la secuencia de grados
print(list(dict(G.degree()).values()))

2
[(0, 1), ('Juan', 0), ((1.2, 3.4), 0), (1, 2), (2, 1), (3, 1), ('Carlos', 0), ('Jorge', 2), ('Camila', 2), (100, 1), (4, 1), ('A', 1), ('B', 1), ('Claudia', 1), ('Concepcion', 1), ('Santiago', 1)]
[1, 0, 0, 2, 1, 1, 0, 2, 2, 1, 1, 1, 1, 1, 1, 1]

G.edges("Jorge")

EdgeDataView([('Jorge', 'Camila'), ('Jorge', 'Claudia')])

Como sabes, en un grafo dirigido (de clase DiGraph) hay dos tipos de grados. Las cosas funcionan tal cual como tu lo esperas: * G.in_degree(node) * G.out_degree(node) # igual que G.degree()

Otras operaciones

• subgraph(G, nbunch) or G.subgraph(nbunch)
  subgrafo de G inducido por los nodos en nbunch

• reverse(G)
  DiGraph con enlaces al revés

• union(G1, G2)
  unión de grafos

• disjoint_union(G1, G2)
  Igual, pero con trata a los nodos de G1 y G2 como distintos

• intersection(G1, G2)
  grafo con solo los enlaces en común entre G1 y G2

• difference(G1, G2)
  grafo con solo los enlaces G1 que no estan en G2

• copy(G) or G.copy()
  copia de G

• complement(G) or G.complement()
  El complemento del grafo G

• convert_to_undirected(G) or G.to_undirected()
  versión no-dirigida de G (un grafo o multigrafo)

• convert_to_directed(G) or G.to_directed()
  versión dirigida de G (un digrafo o multigrafo)

• adjacency_matrix(G)
  Matriz de adjacencia A del grafo G (en formato de matriz sparse; para obtener la matriz completa (con las entradas iguales a cero, usa A.toarray() )

Graph I/O

Habitualmente, tú no construiras una red desde cero, un nodo link a la vez. Por el contrario, tú querras leer un la red desde un archivo. NetworkX puede entender los siguientes formatos de grafos:

• edge lists
• adjacency lists
• GML
• GEXF
• Python ‘pickle’
• GraphML
• Pajek
• LEDA
• YAML

Comencemos: Leyendo un edge list

Coloca el archivo test.txt en tu directorio de trabajo para IPython. Si no sabes el directorio de trabajo puedes accederlo tecleando %pwd

en cualquier celda

%pwd

'/Users/crcandia/Dropbox (Personal)/Cursos_UDD/sitio_networkScience/hands-on/HandsOn_Basics'

Lee en el archivo con las siguientes opciones: * Lineas que comienzan con # son tratadas como comentarios e ignoradas * Usa un objeto Graph para almacenar la data (si la red es no-dirigida)
* La data es separada por espacios blancos (’ ’) * Los nodos deberían ser tratados como enteros (int) * El encoding del texto of the text file containing the edge list is utf-8

# lee una edge list desde el archivo'test.txt'
G = nx.read_edgelist('./Data/test.txt',
                     comments='#',
                     create_using=nx.Graph(), 
                     delimiter=' ', 
                    #  nodetype=int, 
                     encoding='utf-8')

Formatos permitidos

• Pares de nodos sin data 1 2
• Pares de nodos con un diccionario de python 1 2 {weight:7, color:"verde"}

Análisis Básico

Un gran número de análisis básicos pueden ser hechos en una linea usando NetworkX (en general usamos nx como alias) + numpy (en general usamos np como alias) o funciones de python como min, max, etc.

G.degree()

DegreeView({'0': 5, '482': 2, '162': 5, '499': 5, '362': 4, '389': 3, '1': 2, '356': 2, '244': 1, '2': 2, '347': 2, '227': 3, '3': 5, '184': 2, '278': 2, '340': 2, '142': 3, '30': 3, '4': 1, '124': 3, '5': 5, '493': 8, '65': 3, '319': 6, '293': 7, '193': 6, '6': 3, '80': 1, '273': 3, '491': 3, '7': 1, '127': 1, '8': 2, '49': 4, '405': 3, '9': 2, '219': 4, '85': 5, '10': 1, '395': 3, '11': 2, '192': 7, '182': 6, '12': 3, '352': 1, '439': 2, '199': 5, '13': 3, '235': 3, '341': 1, '14': 1, '215': 5, '16': 3, '388': 5, '77': 4, '47': 1, '17': 2, '435': 2, '167': 3, '19': 1, '286': 1, '22': 2, '164': 4, '140': 1, '23': 2, '196': 5, '94': 1, '24': 4, '402': 2, '411': 3, '173': 3, '326': 3, '26': 1, '453': 4, '29': 1, '97': 1, '320': 3, '31': 3, '360': 4, '497': 3, '243': 1, '33': 1, '470': 2, '34': 2, '400': 1, '134': 4, '35': 1, '259': 5, '36': 2, '111': 6, '37': 3, '496': 2, '76': 6, '79': 3, '38': 1, '40': 1, '88': 5, '41': 4, '200': 4, '73': 4, '92': 2, '481': 3, '42': 3, '445': 2, '486': 3, '44': 3, '190': 2, '119': 3, '45': 3, '186': 2, '163': 3, '198': 2, '46': 3, '252': 3, '48': 1, '176': 3, '129': 2, '250': 3, '50': 3, '336': 3, '122': 3, '51': 3, '224': 1, '434': 2, '299': 1, '52': 1, '342': 4, '53': 1, '498': 1, '54': 2, '474': 5, '55': 2, '382': 3, '334': 5, '56': 3, '339': 1, '123': 3, '438': 6, '57': 2, '177': 2, '451': 1, '58': 1, '59': 1, '120': 2, '60': 2, '385': 2, '260': 3, '61': 3, '83': 3, '133': 4, '454': 3, '62': 2, '242': 2, '255': 4, '63': 3, '432': 2, '107': 2, '64': 3, '328': 3, '221': 3, '67': 1, '386': 3, '68': 5, '369': 2, '178': 2, '323': 2, '141': 2, '69': 3, '401': 2, '70': 1, '99': 4, '428': 1, '74': 4, '276': 2, '154': 2, '469': 3, '75': 2, '329': 5, '132': 2, '214': 2, '442': 1, '158': 3, '370': 2, '407': 3, '383': 2, '78': 3, '137': 3, '282': 2, '292': 3, '81': 1, '82': 2, '165': 7, '139': 3, '477': 2, '272': 4, '121': 2, '86': 1, '480': 4, '253': 5, '90': 3, '194': 4, '101': 3, '91': 1, '93': 1, '96': 1, '268': 4, '98': 2, '426': 2, '335': 3, '289': 3, '467': 3, '207': 4, '100': 2, '468': 4, '267': 5, '102': 1, '384': 3, '103': 4, '353': 3, '463': 4, '104': 1, '105': 1, '422': 4, '108': 1, '110': 1, '213': 2, '279': 1, '136': 3, '436': 2, '112': 3, '440': 4, '456': 3, '324': 1, '114': 1, '327': 3, '115': 1, '344': 2, '116': 3, '322': 2, '187': 3, '310': 3, '117': 4, '201': 2, '131': 3, '265': 5, '241': 2, '118': 1, '203': 2, '387': 4, '297': 4, '125': 2, '240': 4, '126': 2, '285': 5, '238': 2, '128': 4, '378': 2, '183': 2, '130': 2, '325': 4, '419': 3, '228': 2, '304': 1, '484': 2, '135': 1, '364': 2, '359': 2, '138': 2, '220': 2, '150': 2, '143': 2, '144': 1, '145': 3, '475': 2, '146': 1, '147': 2, '148': 2, '294': 1, '191': 5, '149': 1, '461': 2, '233': 1, '151': 2, '354': 1, '152': 5, '374': 6, '447': 2, '155': 4, '248': 2, '156': 1, '157': 2, '209': 2, '410': 2, '222': 2, '159': 2, '358': 4, '160': 2, '249': 4, '398': 1, '466': 2, '460': 1, '269': 3, '212': 1, '427': 3, '431': 4, '168': 6, '166': 2, '379': 2, '179': 1, '303': 2, '495': 2, '169': 3, '441': 2, '180': 1, '170': 3, '262': 1, '171': 2, '473': 1, '174': 1, '175': 1, '489': 2, '478': 1, '181': 3, '472': 2, '450': 2, '376': 3, '185': 2, '487': 2, '311': 1, '403': 2, '188': 3, '488': 2, '307': 1, '189': 1, '291': 2, '195': 2, '424': 1, '397': 3, '197': 2, '371': 2, '218': 1, '202': 2, '337': 3, '261': 1, '204': 1, '205': 2, '394': 2, '391': 2, '208': 2, '399': 2, '210': 2, '357': 3, '211': 4, '225': 2, '301': 4, '415': 2, '257': 2, '277': 3, '216': 2, '423': 4, '247': 3, '217': 2, '236': 2, '302': 2, '275': 1, '223': 2, '380': 3, '393': 3, '229': 1, '464': 2, '230': 2, '231': 2, '290': 2, '375': 1, '237': 3, '274': 1, '239': 1, '355': 2, '437': 2, '409': 4, '338': 2, '331': 1, '313': 3, '251': 1, '396': 5, '430': 2, '306': 2, '254': 2, '361': 3, '256': 1, '263': 1, '264': 1, '312': 1, '266': 2, '408': 2, '309': 2, '270': 3, '417': 4, '443': 2, '366': 1, '271': 2, '406': 4, '295': 2, '429': 1, '280': 1, '281': 2, '283': 1, '288': 2, '284': 1, '455': 1, '287': 2, '452': 2, '485': 3, '444': 1, '315': 1, '462': 2, '316': 1, '318': 1, '317': 1, '420': 2, '365': 3, '330': 1, '332': 2, '433': 2, '348': 1, '343': 1, '350': 1, '346': 1, '349': 3, '351': 2, '363': 1, '368': 2, '421': 2, '390': 1, '377': 1, '490': 3, '381': 1, '458': 1, '494': 3, '404': 2, '418': 1, '457': 1, '465': 1})

N = len(G)
L = G.size()
degrees = list(dict(G.degree()).values())
kmin = min(degrees)
kmax = max(degrees)

# degrees

print("Número de nodos: ", N)
print("Número de enlaces: ", L)
print('-------')
print("Grado promedio: ", 2*L/N) #Formula vista en clases (qué sucedía con las redes reales?)
print("Grado promedio (alternativa de calculo)", np.mean(degrees))
print('-------')
print("Grado mínimo: ", kmin)
print("Grado máximo: ", kmax)

Número de nodos:  443
Número de enlaces:  540
-------
Grado promedio:  2.4379232505643342
Grado promedio (alternativa de calculo) 2.4379232505643342
-------
Grado mínimo:  1
Grado máximo:  8

Ploteando la red

• NetworkX puede dibujar redes usando un gran número de algoritmos de “layout” (diseño)
• Los resultados no son tan bonitos como en Gephi, pero NetworkX es mejor para una visualización rápida y no muy pulcra y entrega un control fino sobre el diseño.

G.number_of_edges()

540

# Usando el algoritmo force-based o "spring" 
fig = plt.figure(figsize=(8,8))

nx.draw_spring(G, node_size=40)

# usando el algoritmo circular 
fig = plt.figure(figsize=(8,8))
nx.draw_circular(G, node_size=20)

Ploteando la distribución de grados

Vamos a plotearla en escala logaritmica primero (IMPORTANTE!!!!!)

numpy puede ser usado para hacer bines logaritmicamente espaciados entre el grado mínimo y el grado máximo.

print(kmax)
print(kmin)
print(degrees)

8
1
[5, 2, 5, 5, 4, 3, 2, 2, 1, 2, 2, 3, 5, 2, 2, 2, 3, 3, 1, 3, 5, 8, 3, 6, 7, 6, 3, 1, 3, 3, 1, 1, 2, 4, 3, 2, 4, 5, 1, 3, 2, 7, 6, 3, 1, 2, 5, 3, 3, 1, 1, 5, 3, 5, 4, 1, 2, 2, 3, 1, 1, 2, 4, 1, 2, 5, 1, 4, 2, 3, 3, 3, 1, 4, 1, 1, 3, 3, 4, 3, 1, 1, 2, 2, 1, 4, 1, 5, 2, 6, 3, 2, 6, 3, 1, 1, 5, 4, 4, 4, 2, 3, 3, 2, 3, 3, 2, 3, 3, 2, 3, 2, 3, 3, 1, 3, 2, 3, 3, 3, 3, 3, 1, 2, 1, 1, 4, 1, 1, 2, 5, 2, 3, 5, 3, 1, 3, 6, 2, 2, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 3, 2, 2, 4, 3, 2, 2, 3, 3, 3, 1, 3, 5, 2, 2, 2, 2, 3, 2, 1, 4, 1, 4, 2, 2, 3, 2, 5, 2, 2, 1, 3, 2, 3, 2, 3, 3, 2, 3, 1, 2, 7, 3, 2, 4, 2, 1, 4, 5, 3, 4, 3, 1, 1, 1, 4, 2, 2, 3, 3, 3, 4, 2, 4, 5, 1, 3, 4, 3, 4, 1, 1, 4, 1, 1, 2, 1, 3, 2, 3, 4, 3, 1, 1, 3, 1, 2, 3, 2, 3, 3, 4, 2, 3, 5, 2, 1, 2, 4, 4, 2, 4, 2, 5, 2, 4, 2, 2, 2, 4, 3, 2, 1, 2, 1, 2, 2, 2, 2, 2, 2, 1, 3, 2, 1, 2, 2, 1, 5, 1, 2, 1, 2, 1, 5, 6, 2, 4, 2, 1, 2, 2, 2, 2, 2, 4, 2, 4, 1, 2, 1, 3, 1, 3, 4, 6, 2, 2, 1, 2, 2, 3, 2, 1, 3, 1, 2, 1, 1, 1, 2, 1, 3, 2, 2, 3, 2, 2, 1, 2, 3, 2, 1, 1, 2, 2, 1, 3, 2, 2, 1, 2, 3, 1, 1, 2, 2, 2, 2, 2, 2, 3, 4, 2, 4, 2, 2, 3, 2, 4, 3, 2, 2, 2, 1, 2, 3, 3, 1, 2, 2, 2, 2, 1, 3, 1, 1, 2, 2, 4, 2, 1, 3, 1, 5, 2, 2, 2, 3, 1, 1, 1, 1, 2, 2, 2, 3, 4, 2, 1, 2, 4, 2, 1, 1, 2, 1, 2, 1, 1, 2, 2, 3, 1, 1, 2, 1, 1, 1, 2, 3, 1, 2, 2, 1, 1, 1, 1, 3, 2, 1, 2, 2, 1, 1, 3, 1, 1, 3, 2, 1, 1, 1]

# Generamos 20 bins espaciados logaritmicamente entre kmin y kmax
bin_edges = np.logspace(np.log10(kmin), np.log10(kmax), num=10)#bins en escala lineal con espaciado logaritmico

# histograma de la data para esos bines
density, _ = np.histogram(degrees, bins=bin_edges, density=True)

bin_edges

array([1.        , 1.25992105, 1.58740105, 2.        , 2.5198421 ,
       3.1748021 , 4.        , 5.0396842 , 6.34960421, 8.        ])

# np.histogram(degrees, bins=bin_edges, density=True)

np.log10(bin_edges)

array([0.        , 0.04753105, 0.0950621 , 0.14259316, 0.19012421,
       0.23765526, 0.28518631, 0.33271736, 0.38024842, 0.42777947,
       0.47531052, 0.52284157, 0.57037262, 0.61790368, 0.66543473,
       0.71296578, 0.76049683, 0.80802788, 0.85555894, 0.90308999])

Ahora lo graficamos!

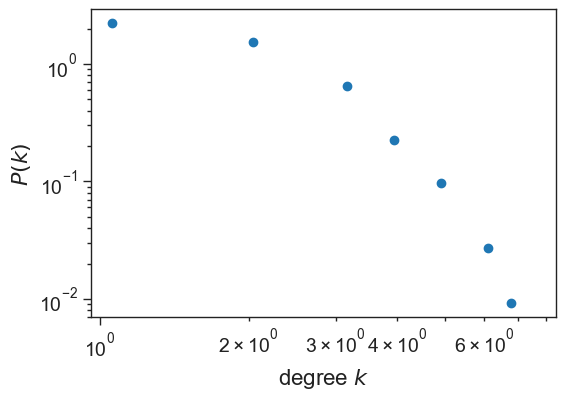
fig = plt.figure(figsize=(6,4))


# "x" debe ser el punto medio (en escala LOG) de cada bin
log_be = np.log10(bin_edges)#debemos hacer el logaritmo para hacer la suma en escala logaritmica
x = 10**((log_be[1:] + log_be[:-1])/2)# calculamos el punto medio (X_i+X_(i+1))/2 y volvemos a la escala anterior.



plt.loglog(x, density, marker='o', linestyle='none')#notacion ejes en logaritmo
plt.xlabel(r"degree $k$", fontsize=16)
plt.ylabel(r"$P(k)$", fontsize=16)

# # remuevo los limites derecho y superior 
# ax = plt.gca()
# ax.spines['right'].set_visible(False)
# ax.spines['top'].set_visible(False)
# ax.yaxis.set_ticks_position('left')
# ax.xaxis.set_ticks_position('bottom')

# Muestra la gráfica
plt.show()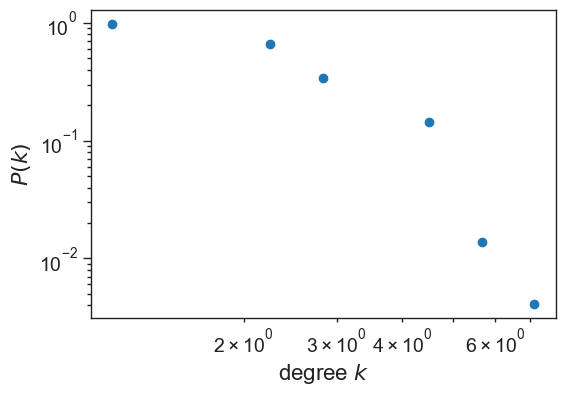

# Chequeamos el espaciado
a=bin_edges[1:] - bin_edges[:-1]
# plt.semilogy(a, color='blue', lw=2)#si el una curva de crecimiento logaritmico, deberia ser una linea recta en un semilog plot
plt.plot(a, color='blue', lw=2)

plt.show()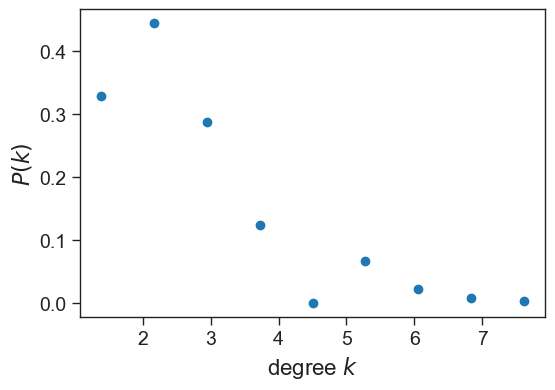

Esto claramente no es una red con algo así como una distribución de grado de ley de potencia o de cola pesada También vamos a graficarla en escala lineal.

El comando linspace de numpy se usa para obtener números linealmente espaciados entre dos extremos.

# Entrega 20 bins linealmente espaceados entre kmin y kmax
bin_edges = np.linspace(kmin, kmax, num=10)

# histograma de la data en estos bines 
density, _ = np.histogram(degrees, bins=bin_edges, density=True)

Ahora lo graficamos!

fig = plt.figure(figsize=(6,4))

# "x" debería ser el punto medio de cada bin

x = ((bin_edges[1:] + bin_edges[:-1])/2)

plt.plot(x, density, marker='o', linestyle='none')
plt.xlabel(r"degree $k$", fontsize=16)
plt.ylabel(r"$P(k)$", fontsize=16)


# Muestra la gráfica
plt.show()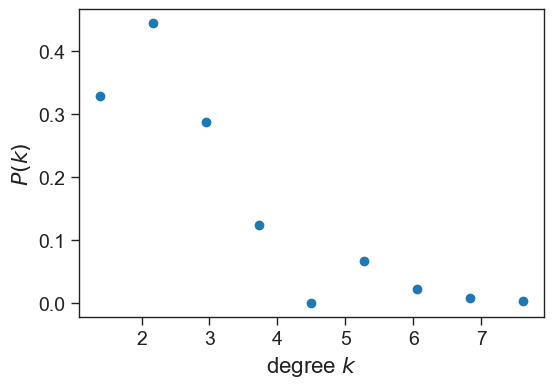

# Chequeamos el espaciado
(bin_edges[1:] - bin_edges[:-1])

array([0.25992105, 0.32748   , 0.41259895, 0.5198421 , 0.65496   ,
       0.8251979 , 1.0396842 , 1.30992001, 1.65039579])

Tarea 1

De manera individual. Tienen una semana para entregar esta tarea. Para ambos datasets example_1.txt y example_2.txt. Cada uno deberá cargar el edge list que corresponde y hacer lo siguiente:

• Pregunta 1: Calcula todas las medidas básicas que se muestran arriba. Comente ¿Qué se puede sospechar acerca de la distribución de grados de la red solo en función de la media y los grados extremos?

• Pregunta 2: Graficar la distribución de grado en escala log-log. También graficarlo en escala lineal. Comente cómo encaja esto con el análisis de la pregunta 1.

• Pregunta 3: Dibuje la red utilizando los dos algoritmos de diseño que se muestran arriba. ¿Cómo se refljan en la apariencia de la red los hallazgos de las preguntas 1 y 2?

Nota: Recuerden que SU interpretación de los resultados es lo más importante.

# Generamos 10 bins espaciados logaritmicamente entre kmin y kmax
bin_edges = np.logspace(np.log10(kmin), np.log10(kmax), num=20)

# histograma de la data para esos bines
density, _ = np.histogram(degrees, bins=bin_edges, density=True)

fig = plt.figure(figsize=(6,4))

# "x" debe ser el punto medio (en escala LOG) de cada bin
log_be = np.log10(bin_edges)
x = 10**((log_be[1:] + log_be[:-1])/2)

plt.loglog(x, density, marker='o', linestyle='none')
plt.xlabel(r"degree $k$", fontsize=16)
plt.ylabel(r"$P(k)$", fontsize=16)

# # remuevo los limites derecho y superior 
# ax = plt.gca()
# ax.spines['right'].set_visible(False)
# ax.spines['top'].set_visible(False)
# ax.yaxis.set_ticks_position('left')
# ax.xaxis.set_ticks_position('bottom')

# Muestra la gráfica
plt.show()