Network Science - UDD

Network metrics

Cristian Candia-Castro Vallejos, Ph.D.1,2

Yessica Herrera-Guzmán, Ph.D.2,3

  • [1] Data Science Institute (IDS), Universidad del Desarrollo,Chile
  • [2] Northwestern Institute on Complex Systems, Kellogg School of Management, Northwestern Unviersity, USA
  • [3] Center for Complex Network Research (CCNR), Northwestern Unviersity, USA
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
%matplotlib inline

import networkx as nx
file_path = "edgelist.txt"
g = nx.Graph()
with open(file_path, "r") as file:
    for line in file:
        # Split each line to extract the node pairs
        nodes = line.strip().split()
        if len(nodes) == 2:
            g.add_edge(nodes[0], nodes[1])
# Fruchterman-Reingold force-directed layout algorithm ~ default
fig = plt.figure(figsize=(6,6))
nx.draw(g, node_size=40)
# if you need labels to check nodes:
# nx.draw(g, node_size=40, with_labels=True)

Three basic properties

N = len(g)
L = g.size()
degrees = list(dict(g.degree()).values())
kmin = min(degrees)
kmax = max(degrees)
print("Number of nodes: ", N)
print("Number of links: ", L)
print('-------')
print("Average degree: ", 2*L/N) #Formula vista en clases (qué sucedía con las redes reales?)
print("Average degree (alternative estimation)", np.mean(degrees))
print('-------')
print("Minimum degree: ", kmin)
print("Maximum degree: ", kmax)
Number of nodes:  197
Number of links:  1651
-------
Average degree:  16.761421319796955
Average degree (alternative estimation) 16.761421319796955
-------
Minimum degree:  1
Maximum degree:  43

Degree distribution

bin_edges = np.logspace(np.log10(kmin), np.log10(kmax), num=20)

# remember to make the histogram!
density, _ = np.histogram(degrees, bins=bin_edges, density=True)
fig = plt.figure(figsize=(4,4))


log_be = np.log10(bin_edges) # log scale
x = 10**((log_be[1:] + log_be[:-1])/2) # (X_i+X_(i+1))/2



plt.loglog(x, density, marker='o', linestyle='none') 
# don't forget axis labels and right size!
plt.xlabel(r"degree $k$", fontsize=16)
plt.ylabel(r"$P(k)$", fontsize=16)



plt.show()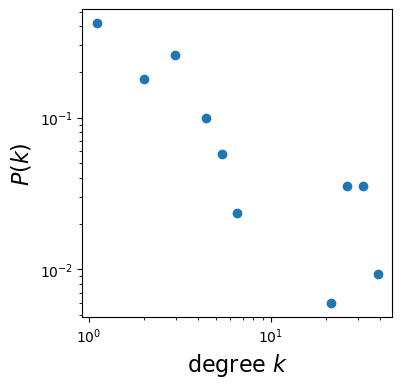

# Check binning
fig = plt.figure(figsize=(4,4))

a=bin_edges[1:] - bin_edges[:-1]

plt.plot(a, color='blue', lw=2)

plt.show()

Path length

nx.average_shortest_path_length(g)
---------------------------------------------------------------------------
NetworkXError                             Traceback (most recent call last)
Input In [117], in <cell line: 1>()
----> 1 nx.average_shortest_path_length(g)

File ~/miniconda3/envs/otro_lumos/lib/python3.8/site-packages/networkx/algorithms/shortest_paths/generic.py:389, in average_shortest_path_length(G, weight, method)
    387     raise nx.NetworkXError("Graph is not weakly connected.")
    388 if not G.is_directed() and not nx.is_connected(G):
--> 389     raise nx.NetworkXError("Graph is not connected.")
    391 # Compute all-pairs shortest paths.
    392 def path_length(v):

NetworkXError: Graph is not connected.

Oh! Grapht is not connected!

How do we measure the average path length, then?

# Explore number of connected components
components = list(nx.connected_components(g))
largest_component = max(components, key=len)
# This is a subgraph of the largest connected component
lc_graph = g.subgraph(largest_component)
nx.average_shortest_path_length(lc_graph)
1.696969696969697
nx.diameter(lc_graph)
2

Quick quizz:

  • How are the average shorthest path and diameter related?

  • What do they measure drom the network structure?

  • How would the diameter change for a random network of N nodes, when changed to a tree-like structure?

  • Compute the size of the largest connected component: number of nodes and edges respect to the entire network.

Clustering coefficient

clustering = nx.clustering(g)
clustering_values = list(clustering.values())
plt.hist(clustering_values, bins=20, alpha=0.7)
plt.xlabel("Clustering Coefficient")
plt.ylabel("Frequency")
plt.title("Clustering Coefficient Distribution")
plt.grid(True)

# Show the histogram
plt.show()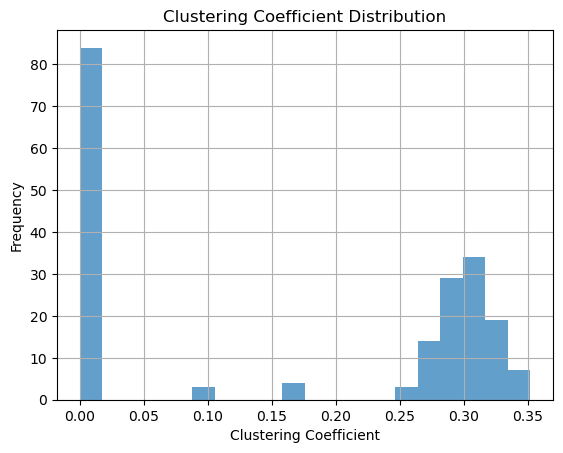

Note that nx.clustering(g) provides the clustering for each node. So you can explore what is the clustering coefficient of specific nodes, for example:

node_id = '87'
cc_node = nx.clustering(g, node_id)
print(f"Clustering coefficient for Node {node_id}: {cc_node}")
Clustering coefficient for Node 87: 0.16666666666666666

Now we know the distribution of the clustering coefficient, let’s compute the average clustering coefficient:

average_cc = nx.average_clustering(g)
print(f"The average clustering coefficient of this network is {average_cc}")
The average clustering coefficient of this network is 0.1682917533972737

Lastly, let’s compute network density:

density = nx.density(g)
print(f"The density of this network is {density}")
The density of this network is 0.08551745571324977

Quick quizz:

  • What is the meaning of a high clustering coefficient?

  • What is the meaning of a low clustering coefficient?

  • How is the density of a network related to clustering coefficient?

  • How does the average clustering coefficient varies by each network model: random, BA, and WS?

  • What insights could you obtain about a network by only knowing that its average clustering coefficient is 0.46 and it has a 30% of random edges?

  • Lastly, describe what is the usefulness of the three network metrics for network analysis.

Network properties of different networks

Erdos-Renyi random graph

num_nodes = 200
# Probability of edge creation (adjust and have fun learning!)
probability = 0.2
er = nx.erdos_renyi_graph(num_nodes, probability)
fig = plt.figure(figsize=(6,6))
nx.draw(er, node_size=40)

Watts-Strogatz small-world graph

num_nodes = 200
# Number of nearest neighbors to connect
k = 4
# Probability of rewiring each edge
p = 0.1
ws = nx.watts_strogatz_graph(num_nodes, k, p)
fig = plt.figure(figsize=(6,6))
nx.draw(ws, node_size=40)

Barabási-Albert graph

num_nodes = 200
# Number of edges to attach from a new node to existing nodes ~ Hubs!
m = 3
ab = nx.barabasi_albert_graph(num_nodes, m)
fig = plt.figure(figsize=(6,6))
nx.draw(ab, node_size=40)

Moving on:

  • Compute the network properties studied here for each of these networks.

  • Describe whether the three central metrics can be characteristic of each model.

  • Discuss the limitations of the metrics and what other metrics could be computed to understand the network and nodes’ relationships in more detail.